The human perception of time is logarithmic. We have words like second, minute, hour, day, week, month, year, decade, century, millennium etc. to refer to exponentially increasing time frames. But despite this fact, plots over time are usually in linear scale. When looking at values like the CPU load, the frame update time of a game, or the response time of a server, the last few seconds are of interest but at the same time the course of the last hours or days are valuable information. In order to display this range of time in appropriate detail, a linear plot is not sufficient.
Instead here, I introduce a combined linear and logarithmic plot. Short times are displayed in a linear time axis and longer time frames in (compressed) logarithmic time axis.
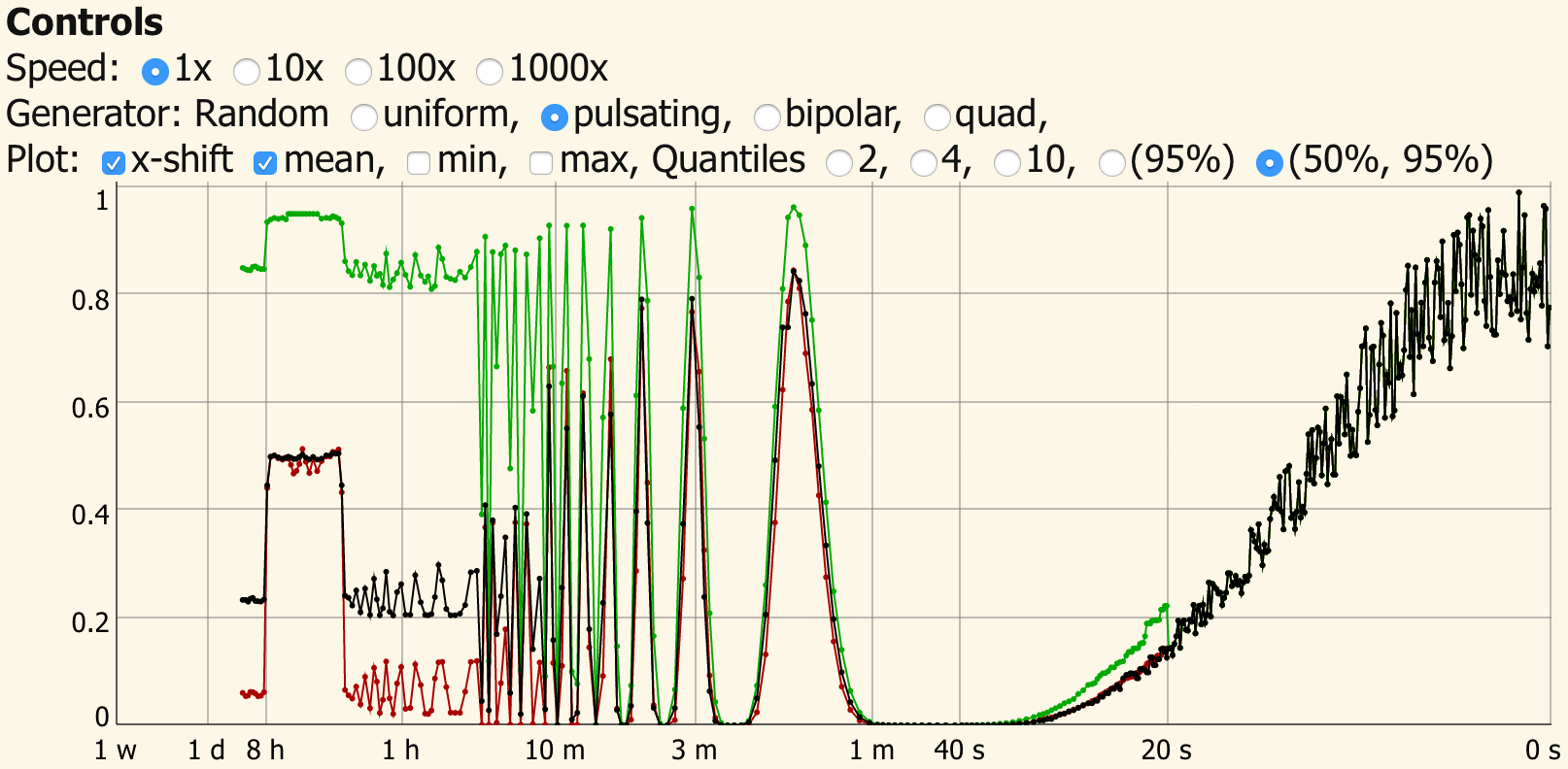
Example of the linear and logarithmic plot. Read the full article for a live demo.
One problem that arises when plotting is that in a week there are 604800 seconds. This would make updating such a plot very time consuming and impractical for responsive applications. To solve this, I reduce the time values in a logarithmic fashion by recursively combining two values to a single one. Combining two values to a single one is simple for the mean, the minimum and maximum value of a time series. In this case, the average, largest and smallest value of both samples which are to be combined are kept.
In the case of CPU load, the minimum over a time period will always be 0 %, the maximum will be 100 % and the mean value does not express sufficiently how heavily e.g. a web-server is loaded. Here, another value like the 95th-percentile of the load histogram gives an idea how much time the server spent under high load. The median (or 50th-percentile) usually coincides well with the mean, except when the distribution function is heavily skewed. In the case of a web-server the median can give an idea of the base load by background processes. Combining two histograms, however, requires a bit more thought than simply calculating the average of two values.
Read on for a live demo and illustrations which explain the method.
more